MOPS® is a high performance software system for solving large-scale linear (LP), integer and mixed-integer optimization models (IP).

MOPS is based on state-of-the-art algorithms and their efficient implementation; key features are:

• Advanced LP-preprocessing algorithms to remove redundancies in LP/IP-models
• Primal and dual simplex algorithms with efficient LU-technology and various pricing strategies
• Fast Interior point (barrier) algorithm with optimal basis identification
• a new state-of-the-art dual simplex engine which is frequenty the fastes LP-engine
• Supernode processing for IP-models is designed to strengthen the LP-relaxation of the IP-model

MOPS is a proven system  - used in applications of large companies since 1990. It is available on nearly all system platforms (Windows, UNIX, OS/390, VM/CMS, BS2000/OSD).

The benchmark results with MOPS for specific public LP/IP-models speak for themselves.

The MOPS team is devoted to deliver top quality products and exceptional service.

 

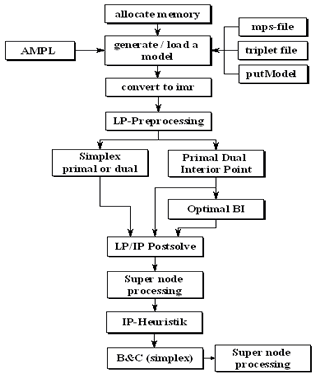
Overview of a typical LP/IP-optimization with MOPS

The following picture shows the normal case of optimizing a model with MOPS. The LP-model is solved after LP-preprocessing either with the interior point (IPM)- or the simplex method. If IPM is used an optimal basis solution can be determined (Optimal BI). A postsolve module determines from the optimal solution of the reduced model an optimal solution of the original model.

If the model contains integer or 0-1 variables a supernode processing is performed to tighten the LP-relaxation before and (optional during) the branch-and-bound-algorithm. Supernode processing encompasses a number of techniques such as:

• Testing and fixing of variables
• Bound and coefficient reduction
• Probing on 0-1-variables
• Deriving cliques and implications, storing cliques- and implications in tables
• Generation of violated cliques, implication, cover, flow and gomory cuts
• Special fixed-charge reduction

In the normal case a heuristic with various rounding options is used to find an initial integer solution.

The branch-and-bound / cut process is based on solving repeatedly LP-models with reduced bounds of some integer variables by either primal or dual simplex method. Modified bounds and optimal bases are normally stored in compressed form in main memory. If the size of the area for storing bounds and bases is exceeded data is automatically moved to disk. The search is limited only by the available disk space and a possible time limit.